


Next: Distribution List
Up: SAND2003-8631 Unlimited Release Printed
Previous: Conclusions
Contents
- 1
-
PAPI: Performance Application Programming Interface.
http://icl.cs.utk.edu/projects/papi/.
- 2
-
PCL -- The Performance Counter Library.
http://www.fz-juelich.de/zam/PCL/.
- 3
-
Sameer Shende, Allen D. Malony, Craig Rasmussen, and Matt Sottile.
A Performance Interface for Component-Based Applications.
In Proceedings of International Workshop on Performance
Modeling, Evaluation and Optimization, International Parallel and Distributed
Processing Symposium, 2003.
- 4
-
Darren J. Kerbyson, Henry J. Alme, Adolfy Hoisie, Fabrizio Petrini, Harvey J.
Wasserman, and Michael L. Gittings.
Predictive performance and scalability modeling of a large-scale
application.
In Proceedings of Supercomputing, 2001.
Distributed via CD-ROM.
- 5
-
Darren J. Kerbyson, Harvey J Wasserman, and Adolfy Hoisie.
Exploring advanced architectures using performance prediction.
In International Workshop on Innovative Architectures, pages
27-40. IEEE Computer Society Press, 2002.
- 6
-
R. Englander and M. Loukides.
Developing Java Beans (Java Series).
O'Reilly and Associates, 1997.
http://www.java.sun.com/products/javabeans.
- 7
-
CORBA Component model webpage.
http://www.omg.com.
Accessed July 2002.
- 8
-
B. A. Allan, R. C. Armstrong, A. P. Wolfe, J. Ray, D. E. Bernholdt, and J. A.
Kohl.
The CCA core specifications in a distributed memory SPMD
framework.
Concurrency: Practice and Experience, 14:323-345, 2002.
Also at http://www.cca-forum.org/ccafe03a/index.html.
- 9
-
Rob Armstrong, Dennis Gannon, Al Geist, Katarzyna Keahey, Scott R. Kohn, Lois
McInnes, Steve R. Parker, and Brent A. Smolinski.
Toward a Common Component Architecture for High-Performance
Scientific Computing.
In Proceedings of High Performance Distributed Computing
Symposium, 1999.
- 10
-
Sophia Lefantzi, Jaideep Ray, and Habib N. Najm.
Using the Common Component Architecture to Design High Performance
Scientific Simulation Codes.
In Proceedings of International Parallel and Distributed
Processing Symposium, 2003.
- 11
-
Sameer Shende, Allen D. Malony, and Robert Ansell-Bell.
Instrumentation and measurement strategies for flexible and portable
empirical performance evaluation.
In Proceedings of the International Conference on Parallel and
Distributed Processing Techniques and Applications, PDPTA '2001, pages
1150-1156. CSREA, June 2001.
- 12
-
Jim Maloney.
Distributed COM Application Development Using Visual C++ 6.0.
Prentice Hall PTR, 1999.
ISBN 0130848743.
- 13
-
Adrian Mos and John Murphy.
Performance Monitoring of Java Component-oriented
Distributed Applications.
In IEEE 9th International Conference on Software,
Telecommunications and Computer Networks - SoftCOM, 2001.
- 14
-
Baskar Sridharan, Balakrishnan Dasarathy, and Aditaya Mathur.
On Building Non-Intrusive Performance Instrumentation
Blocks for CORBA-based Distributed Systems.
In 4th IEEE International Computer Performance and Depenability
Symposium, March 2000.
- 15
-
Baskar Sridharan, Sambhrama Mundkur, and Aditaya Mathur.
Non-intrusive Testing, Monitoring and Control of Distributed
CORBA Objects.
In TOOLS Europe 2000, June 2000.
- 16
-
Nathalie Furmento, Anthony Mayer, Stepen McGough, Steven Newhouse, Tony Field,
and John Darlington.
Optimisation of Component-based Applications within a Grid
Environment.
In Proceedings of Supercomputing, 2001.
Distributed via CD-ROM.
- 17
-
Nathalie Furmento, Anthony Mayer, Stepen McGough, Steven Newhouse, Tony Field,
and John Darlington.
ICENI: Optimisation of Component Applications within a Grid
Environment.
Parallel Computing, 28:1753-1772, 2002.
- 18
-
TAU: Tuning and Analysis Utilities.
http://www.cs.uoregon.edu/research/paracomp/tau/.
- 19
-
Allen D. Malony and Sameer Shende.
Distributed and Parallel Systems: From Concepts to
Applications, chapter Performance Technology for Complex Parallel and
Distributed Sys tems, pages 37-46.
Kluwer, Norwell, MA, 2000.
- 20
-
R. Samtaney and N.J. Zabusky.
Circulation deposition on shock-accelerated planar and curved density
stratified interfaces : Models and scaling laws.
J. Fluid Mech., 269:45-85, 1994.
- 21
-
M. J. Berger and J. Oliger.
Adaptive mesh refinement for hyperbolic partial differential
equations.
J. Comp. Phys., 53:484-523, 1984.
- 22
-
M. J. Berger and P. Collela.
Local adaptive mesh refinement for shock hydrodynamics.
J. Comp. Phys., 82:64-84, 1989.
- 23
-
James J. Quirk.
A parallel adaptive grid algorithm for shock hydrodynamics.
Applied Numerical Mathematics, 20, 1996.
Figure 1:
The density field plotted for a Mach 1.5 shock interacting with an interface
between Air and Freon. The simulation was run on a 3-level grid hierarchy.
Purple patches are the coarsest (Level 0), red ones are on Level 1 (refined once
by a factor of 2) and blue ones are twice refined.
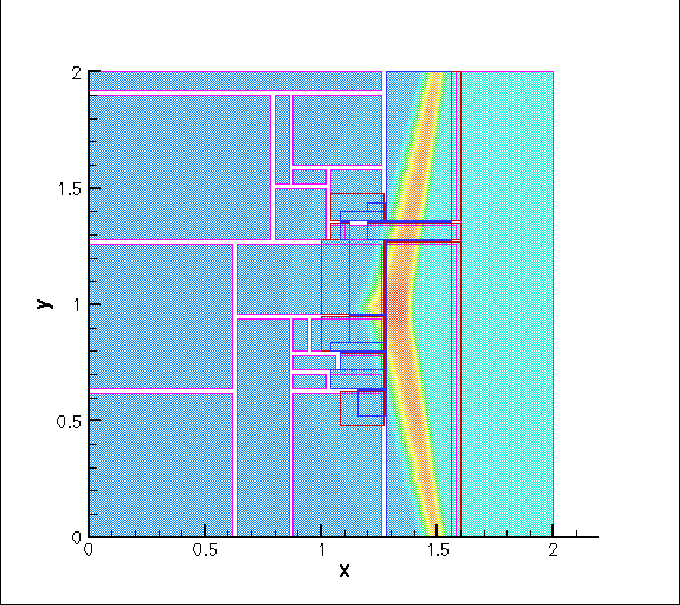 |
Figure 2:
Snapshot of the component application, as assembled for execution. We see
three proxies (for AMRMesh, EFMFlux and States), as well as the
TauMeasurement and Mastermind components to measure and record
performance-related data.
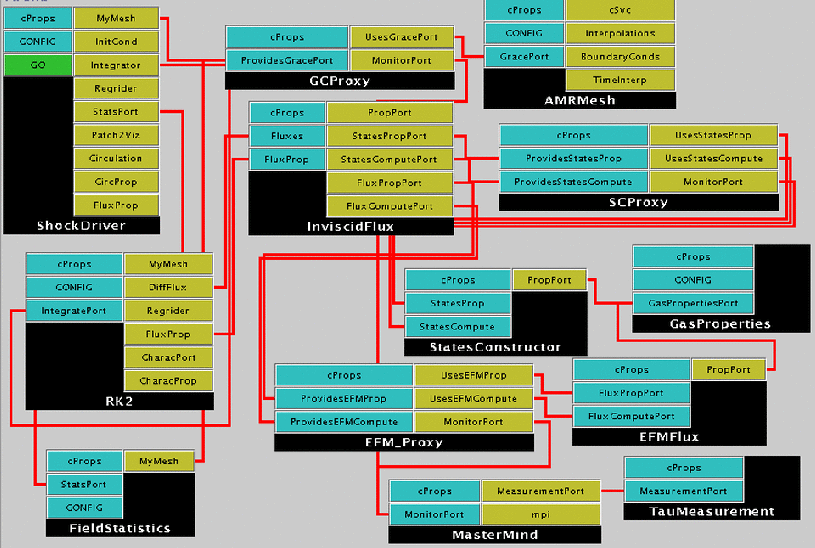 |
Figure 3:
Snapshot from a timing profile done with our infrastructure. We see that
around 50% of the time is accounted for by g_proxy::compute(),
sc_proxy::compute() and MPI_Waitsome(). The MPI call is
invoked from AMRMesh. The two other methods are modeled as a part
of the work reported here. Timings have been averaged over all the processors.
The profile shows the inclusive time (total time spent in the methods and all subsequent
method calls), exclusive time (time spent in the specific method less the time spent in
subsequent instrumented methods), the number of times the method was invoked,
and the average time per call to the method, irrespective of the data being passed into
the method.
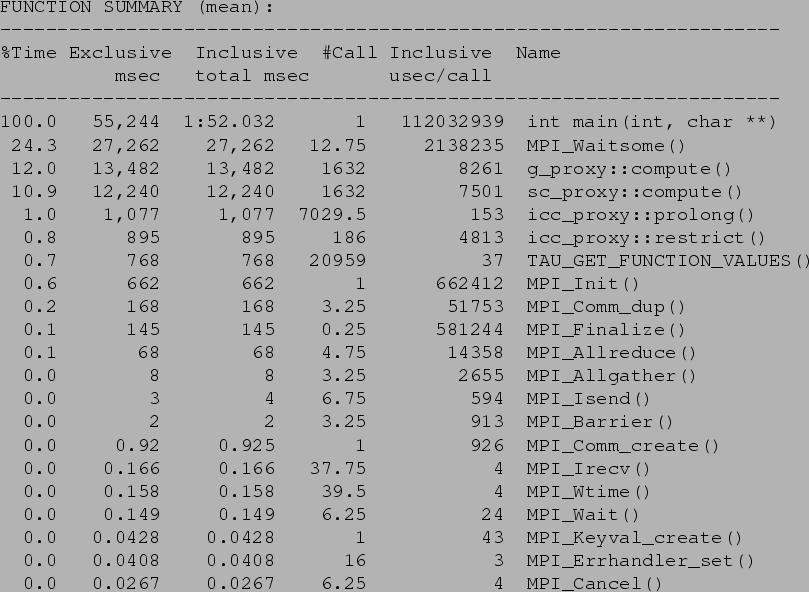 |
Figure 4:
Execution time for the States component. The States component is
invoked in two modes, one which requires sequential and the other which requires
strided access of arrays to calculate X- and Y- derivatives of a field.
Both the times are plotted. The Y-derivative calculation (strided access) is expected
to take longer for large arrays and this is seen in the spread of timings. For small array
sizes, which are largely cache-resident, the two different modes of access do not result
in a large difference in execution time. Array sizes are the actual number of elements
in the array. The elements are double precision numbers. The different colors represent data
from different processors (Proc 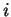 in the legend) and similar trends are seen on all
processors.
in the legend) and similar trends are seen on all
processors.
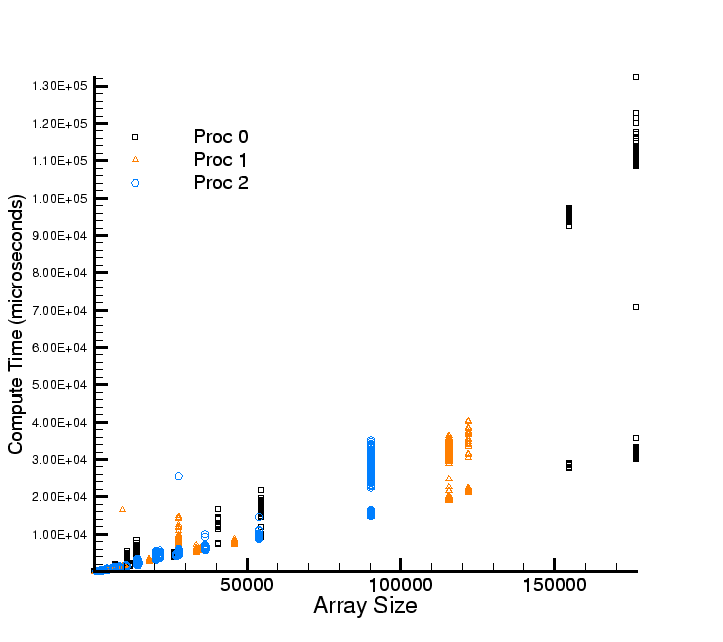 |
Figure 5:
Ratio of strided versus sequential access (calculation of Y- and X-derivatives,
respectively) timings for States. We see that the
ratio varies from around 1 for small array sizes to around 4 for the largest arrays considered
here. Array sizes are the actual number of elements in the array. The elements are
double precision numbers. Further, the ratios show variability which tend to increase with
array size
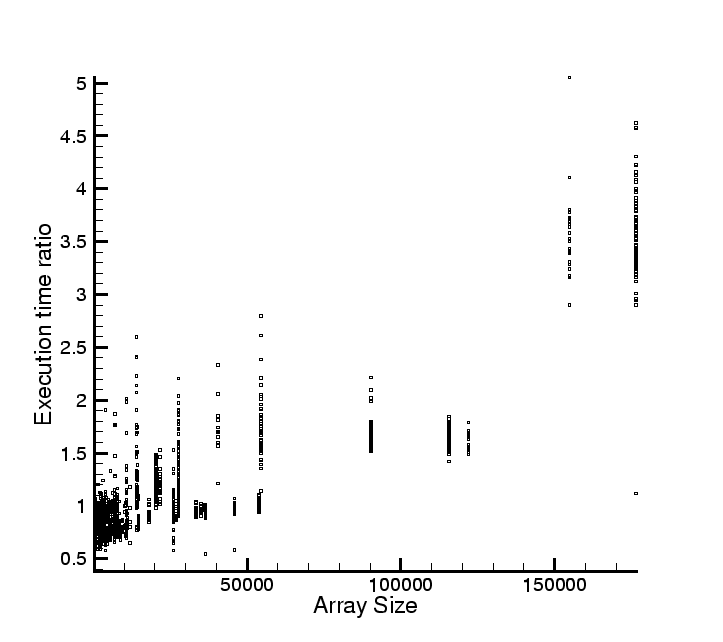 |
Figure 6:
Average execution time for States as a function of the array size. Since
States has a dual mode of operation (sequential versus strided) and the mean includes
both, the standard deviation of is rather large. The performance model is given in
Eq. 1. The standard deviation, in blue, is plotted against the right Y-axis.
All timings are in microseconds.
 |
Figure 7:
Average execution time for GodunovFlux as a function of the array size. Since
GodunovFlux has a dual mode of operation (sequential versus strided) and the mean includes
both, the standard deviation of is rather large. The performance model is given in
Eq. 1. The standard deviation, in blue, is plotted against the right Y-axis.
All timings are in microseconds.
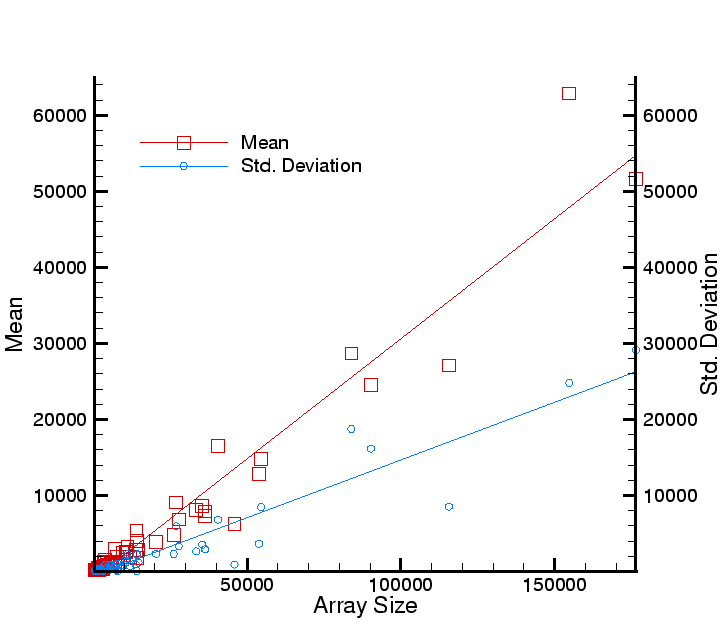 |
Figure 8:
Average execution time for EFMFlux as a function of the array size. Since
EFMFlux has a dual mode of operation (sequential versus strided) and the mean includes
both, the standard deviation of is rather large. The performance model is given in
Eq. 1. The standard deviation, in blue, is plotted against the right Y-axis.
All timings are in microseconds.
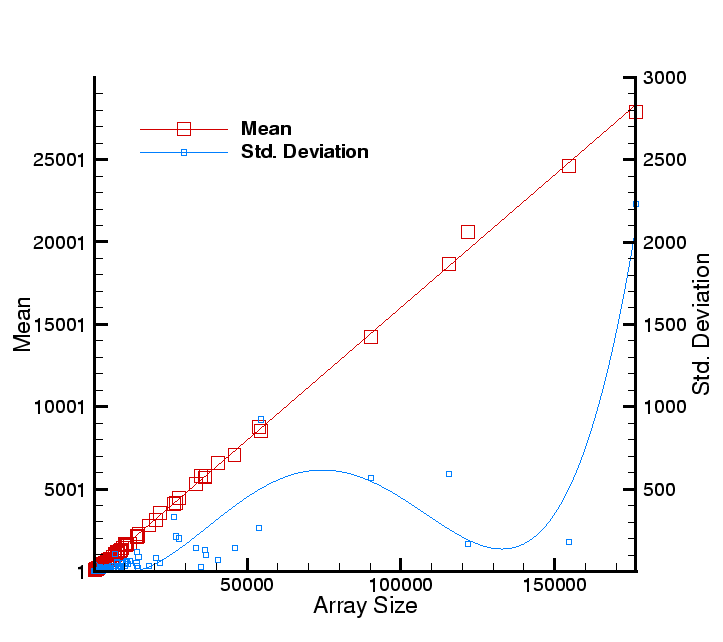 |
Figure 9:
Message passing time for different levels of the grid hierarchy for the 3 processors.
We see a clustering of message passing times, especially for Levels 0 and 2. The grid
hierarchy was subjected to a re-grid step during the simulation which resulted in a different
domain decomposition and consequently message passing times. Inset : We plot the timings for
all processors. Similar clustering is observed. All times are in microseconds.
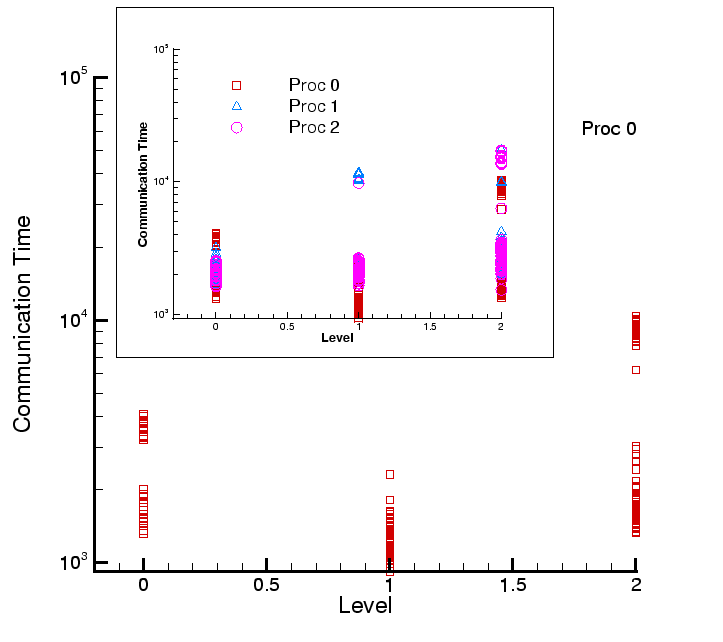 |
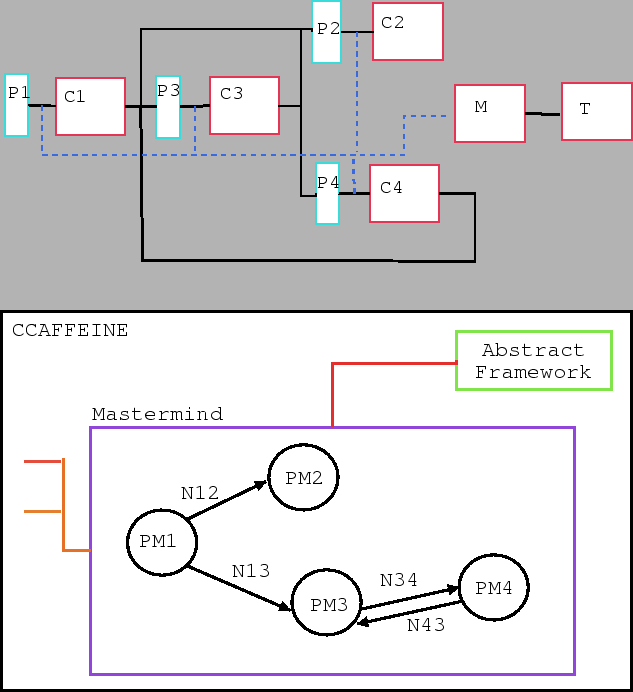
Figure 10:
Above: A simple application composed of 4 components. C denotes a component, P denotes
a proxy and M and T denote an instance of Mastermind and TauMeasurement components.
The black lines denote port connection between components and the blue dashed lines are
the proxy-to-Mastermind port connections which are only used for PMM.
Below, it dual, constructed as a directed graph in the Mastermind, with edge weights
corresponding to the number of invocations and the vertex weights being the compute and
communication times determined from the performance models (PM ) for component
) for component 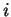 .
Only the port connections shown in black in the picture above are represented in the graph.
The parent-child relationship is preserved to identify sub-graphs that do not
contribute much to the execution time and thus can be neglected during component
assembly optimization. The Mastermind is seen connected to CCAFFEINE via the
AbstractFramework Port to enable dynamic replacement of sub-optimal components.
.
Only the port connections shown in black in the picture above are represented in the graph.
The parent-child relationship is preserved to identify sub-graphs that do not
contribute much to the execution time and thus can be neglected during component
assembly optimization. The Mastermind is seen connected to CCAFFEINE via the
AbstractFramework Port to enable dynamic replacement of sub-optimal components.
 |



Next: Distribution List
Up: SAND2003-8631 Unlimited Release Printed
Previous: Conclusions
Contents
2003-11-05










