


Next: Optimized Code
Up: Debugging
Previous: Reverse Execution and
Most sequential debugging tools provide support for conditional
breakpoints, which halt the program whenever a predicate condition is
satisfied. There are several interpretations of the parallel
equivalent to this feature. Miller and Choi[Mil88] discuss
this issue in detail, and present definitions of distributed
predicates, with an algorithm to detect them and an algorithm to halt
the system after detection. A simple predicate (SP) depends on the
state and execution flow of a single process. Disjunctive (DP) and
conjunctive predicates (CP) are combinations of SPs across processes.
A linked predicate (LP) is specified as a sequence of simple or
disjunctive predicates.
Simple predicates are detectable by sequential debuggers. Disjunctive
predicates are equally trivial to detect (since only one SP must be
detected), but the problem of halting the distributed program in a
consistent state is not trivial. Linked predicates, which are similar
to chains in Ariadne[Kun96], can be detected using an
algorithm presented in [Mil88].
Detection of conjunctive predicates is somewhat more difficult. With
no single global time, it's impossible to say that n SPs are true at
the same time, so a CP must be defined according to the partial
ordering provided by Lamport's happened before relation. For
two processes 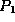 and
and 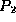 , a set of virtual time pairs
, a set of virtual time pairs 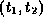 is defined such that
is defined such that 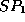 is true at time
is true at time 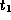 and
and 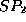 is true
at time
is true
at time 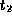 . Then the conjunction
. Then the conjunction 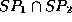 is true at
time-pair
is true at
time-pair 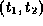 if this time-pair is consistent with the Lamport
partial ordering. Pairs that are ordered can be detected with Linked
predicates. Pairs that are not ordered cannot be consistently
detected except with the use of tracing and replay--see
[Man92].
if this time-pair is consistent with the Lamport
partial ordering. Pairs that are ordered can be detected with Linked
predicates. Pairs that are not ordered cannot be consistently
detected except with the use of tracing and replay--see
[Man92].
If the ZPL were implemented on a fine-grained parallel machine where a
separate thread could be spawned for each region element, Miller and
Choi's algorithms could be used, unmodified, for predicate breakpoint
detection. However, the presence of mloops in the object code
further complicates the issue of detecting conjunctive predicates, as
well as the issue of halting the computation in a consistent state.



Next: Optimized Code
Up: Debugging
Previous: Reverse Execution and
Steve McLaughry
Fri May 30 15:48:07 PDT 1997
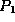 and
and 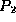 , a set of virtual time pairs
, a set of virtual time pairs 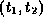 is defined such that
is defined such that 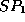 is true at time
is true at time 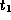 and
and 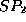 is true
at time
is true
at time 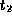 . Then the conjunction
. Then the conjunction 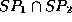 is true at
time-pair
is true at
time-pair 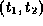 if this time-pair is consistent with the Lamport
partial ordering. Pairs that are ordered can be detected with Linked
predicates. Pairs that are not ordered cannot be consistently
detected except with the use of tracing and replay--see
[Man92].
if this time-pair is consistent with the Lamport
partial ordering. Pairs that are ordered can be detected with Linked
predicates. Pairs that are not ordered cannot be consistently
detected except with the use of tracing and replay--see
[Man92].