



TAU portable profiling and tracing package now supports the following OpenMP implementations:
% configure -TRACE -c++=guidec++ -cc=guidec -openmp -mpiinc=/usr/include -mpilib=/usr/lib32
% setenv OMP_NUM_THREADS 6
% mpirun geos 1, aeros 1 stommel
% tau_merge *.trc stommel.trc
% tau_convert stommel.trc tau.edf stommel.pv
% vampir stommel.pv
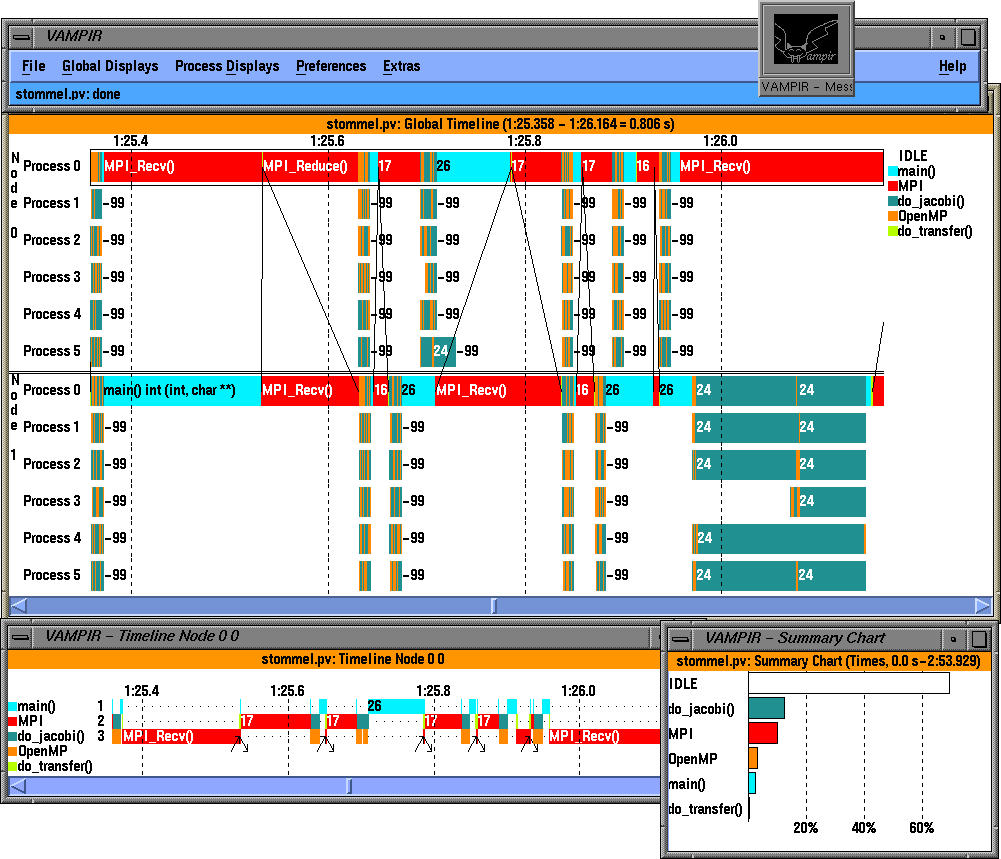
The above figure shows a global timeline display in Vampir. Note that each OpenMP thread is shown distinctly within the SMP node and MPI events are integrated in the trace. TAU can accurately track the precise thread with which inter-process communicatation events are associated.
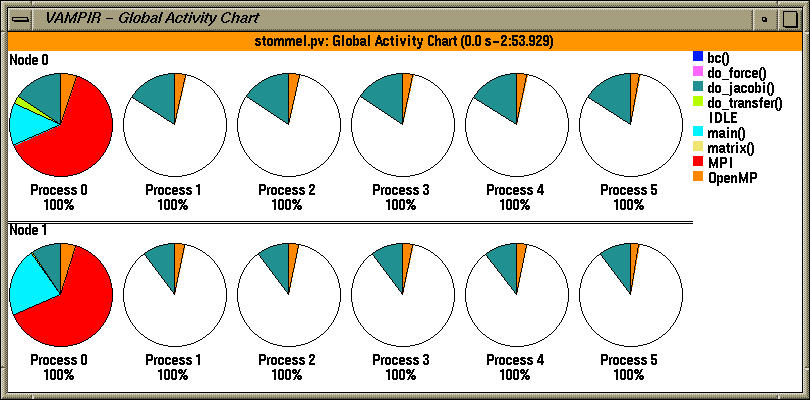
The Global activity display in Vampir shows the breakdown of activities with respect to each thread of execution.
Here, we see a global timeline display of a trace generated by TAU. It highlights an integrated hybrid execution model comprising of MPI (all MPI routines and messages) and OpenMP events (OpenMP parallel regions and loops). Each OpenMP thread is shown independently on the timeline and we see the load imbalance and when and where it takes place. Inter-process communication events are shown at the level of each thread. Although MPI layer does not have any information about the sending and receiving thread, TAU can match sends and receives and generate a Vampir trace where the precise thread involved in the synchronization operation is shown. So, the display shows the global timeline along the X axis and the MPI tasks and threads grouped within the tasks along the Y axis. Also, TAU uses a high level grouping of all events, so in the left, we can see the contribution of all "MPI" routines.
In the Global Activity Chart, we see a pie chart that shows the color coded contribution of each code segment on each OpenMP thread within the two MPI tasks.
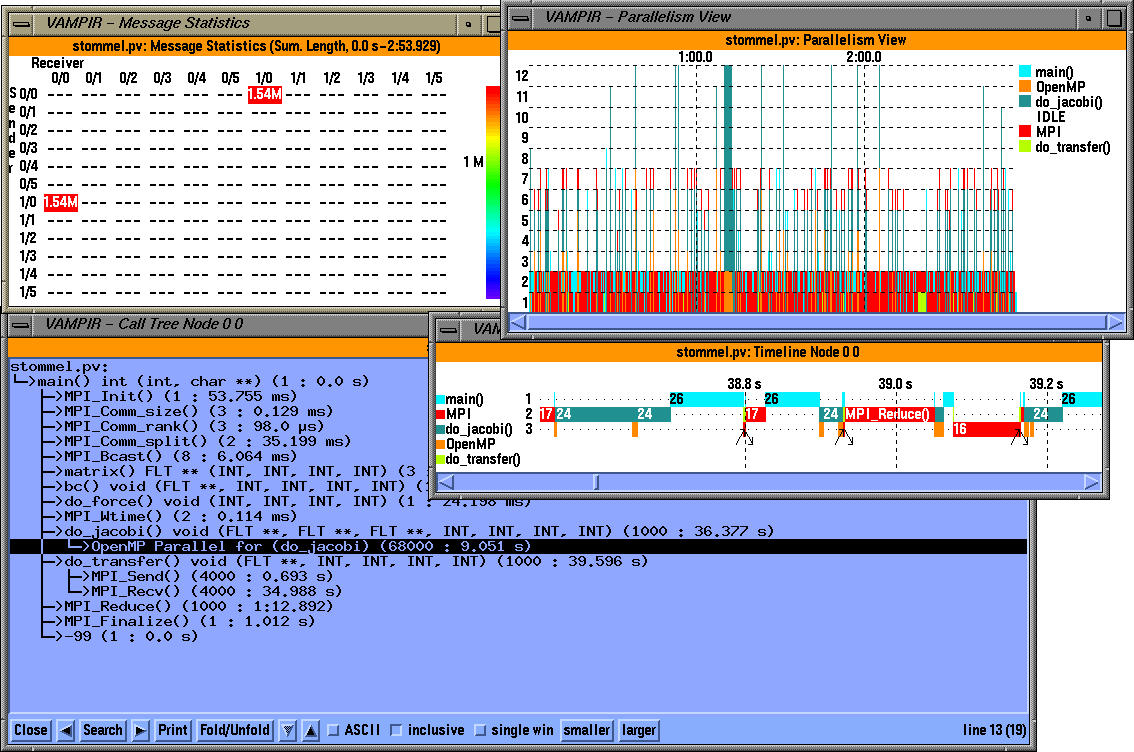
The third display shows several windows. In the top left corner we see a message statistics display in the form of a matrix. Sender nodes and threads are along the y axis and receiver node and threads are along the x axis of this matrix. The extent of communication (Red stands for the most) is shown by a number in the appropriate row and column. In this case, it shows that 1.54MB was exchanged between node 1 thread 0 and node 0 thread 0.
The top left window shows the parallelism view that shows the number of threads that execute a color coded traced region with respect to time. A Timeline display on a particular thread (Node 0, thread 0) shows the level of nesting with respect to time and shows when interprocess communication events take place. Finally, the bottom window shows a dynamic callgraph on a node 0, thread 0. Here we can see MPI routines integrated with OpenMP regions (Parallel for in do_jacobi is highlighted) annotated with performance metrics. In this case, it shows that the OpenMP Parallel for region was invoked 68000 times and it took 9.051 secs of "inclusive" time to execute.
% configure -papi=/usr/local/packages/papi -openmp -c++=pgCC -cc=pgcc -mpiinc=/usr/local/packages/mpich/include -mpilib=/usr/local/packages/mpich/libo
% setenv OMP_NUM_THREADS 2
% setenv PAPI_EVENT PAPI_FP_INS
To set the number of concurrent threads and the hardware performance monitor event prior to running the program. This application was run on a dual Pentium II machine and it generated the performance data shown below.
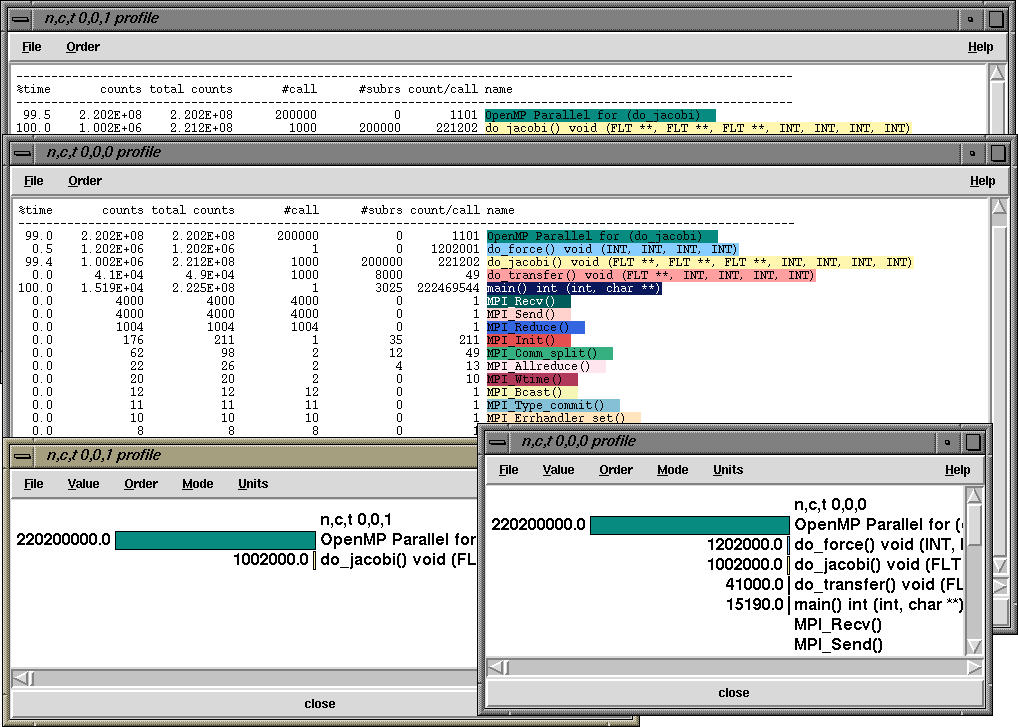
In Scenario 2, we see a Racy display of performance data. TAU can generate detailed event logs that can be visualized in Vampir (Scenario 1) as well as aggregate summary statistics of performance metrics in the form of profiles. The display shows four profile windows. The text based profile display (as in a typical prof output) is color coded for each MPI routine and OpenMP code segment and shows summary statistics. TAU allows the user to choose between profiling with wallclock times, CPU time, Process Virtual Time and Hardware Performance Counts. TAU can use PCL or PAPI to access hardware performance counters. In this case, the text window shows inclusive and exclusive counts of a selected event ( floating point instructions executed, PAPI_FP_INS). So, the third routine do_jacobi, on node 0, context 0, thread 0 executes 1.002E+6 floating point instructions exclusively (of called routines), 2.212E08 inclusive counts, it is called 1000 times (#calls) and it in turn calls 8000 routines (#subrs) and each invocation of this routine calls 221202 floating point instructions on an average. The other window "n,c,t 0,0,1 profile", shows the floating point instructions executed all all profiled routines on node 0, context 0, and thread 1. To its right is a similar display showing bar-graph histograms for exclusive counts for all routines that executed on thread 0. All these displays highlight how MPI events and OpenMP events can be seamlessly integrated in consistent performance views that present detailed information about each thread of execution.
The application uses OpenMP for loop level parallelism in an MPI program and was written by Timothy Kaiser (SDSC). It solves the 2d Stommel Model of Ocean Circulation using a Five-point stencil and Jacobi iteration
gamma*((d(d(psi)/dx)/dx) + (d(d(psi)/dy)/dy))
+beta(d(psi)/dx)=-alpha*sin(pi*y/(2*ly))