TAU supports PAPI with OpenMP + MPI programs now

Examining the total floating point instructions of an OpenMPI program

We illustrate source code instrumentation with MPI wrapper library level instrumentation in TAU. PAPI is used for reading hardware performance counters. We configure TAU using:


% configure -papi=/usr/local/packages/papi -openmp -c++=pgCC -cc=pgcc -mpiinc=/usr/local/packages/mpich/include -mpilib=/usr/local/packages/mpich/libo

% setenv OMP_NUM_THREADS 2
% setenv PAPI_EVENT PAPI_FP_INS

To set the number of concurrent threads and the hardware performance monitor event prior to running the program. This application was run on a dual Pentium II machine and it generated the performance data shown below.

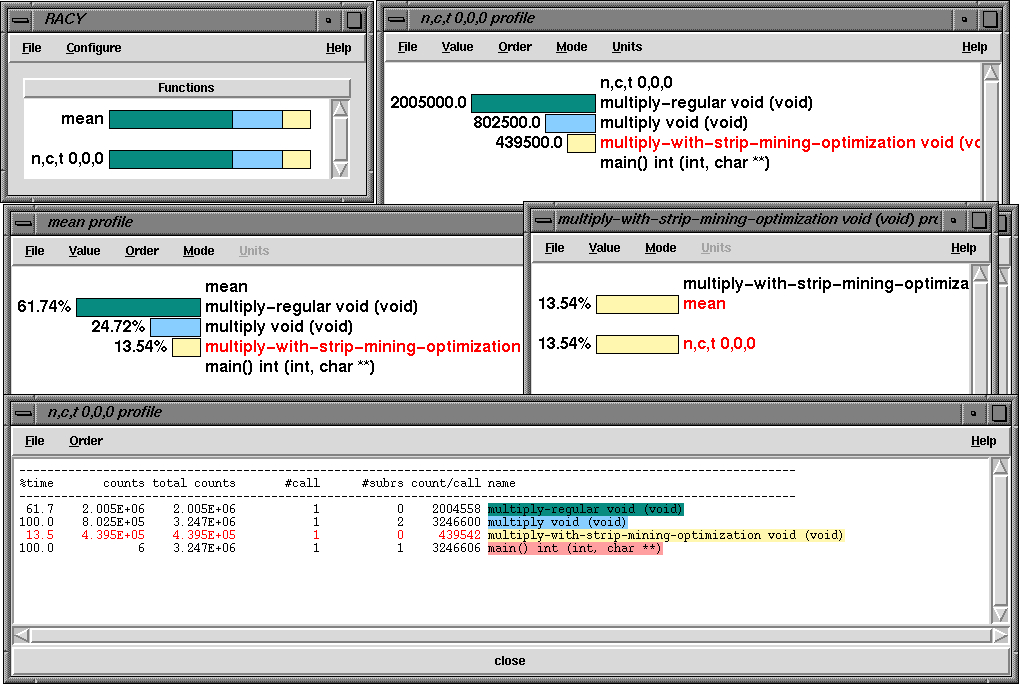
The application uses OpenMP for loop level parallelism in an MPI program and was written by Timothy Kaiser (SDSC). It solves the 2d Stommel Model of Ocean Circulation using a Five-point stencil and Jacobi iteration


 gamma*((d(d(psi)/dx)/dx) + (d(d(psi)/dy)/dy))
 +beta(d(psi)/dx)=-alpha*sin(pi*y/(2*ly))

Examining the total floating point instructions

We illustrate the use of TAU with PAPI by looking at the NAS Parallel Benchmark suite LU. We configure TAU using:


% configure -arch=sgi64 -papi=/research/paraducks/apps/papi -mpiinc=/local/apps/mpich/include -mpilib=/local/apps/mpich/lib/IRIX64/ch_p4 
% setenv PAPI_EVENT PAPI_FP_INS
% mpirun -np 4 lu.W.4
 NAS Parallel Benchmarks 2.2 -- LU Benchmark

 Size:  33x 33x 33
 Iterations: 300
 Number of processes:     4

 Time step    1
 Time step   20
 Time step   40
 Time step   60
 Time step   80
 Time step  100
 Time step  120
 Time step  140
 Time step  160
 Time step  180
 Time step  200
 Time step  220
 Time step  240
 Time step  260
 Time step  280
 Time step  300

 Verification being performed for class W
 Accuracy setting for epsilon =  0.1000000000000E-07
 Comparison of RMS-norms of residual
           1   0.1236511638192E+02 0.1236511638192E+02 0.1465318983036E-12
           2   0.1317228477799E+01 0.1317228477799E+01 0.3777643499391E-12
           3   0.2550120713095E+01 0.2550120713095E+01 0.9194823664494E-13
           4   0.2326187750252E+01 0.2326187750252E+01 0.1846086008657E-12
           5   0.2826799444189E+02 0.2826799444189E+02 0.1519467837203E-12
 Comparison of RMS-norms of solution error
           1   0.4867877144216E+00 0.4867877144216E+00 0.5074586224359E-13
           2   0.5064652880982E-01 0.5064652880982E-01 0.9426033961409E-13
           3   0.9281818101960E-01 0.9281818101960E-01 0.1584867847515E-13
           4   0.8570126542733E-01 0.8570126542733E-01 0.8096606122801E-14
           5   0.1084277417792E+01 0.1084277417792E+01 0.2568013775875E-12
 Comparison of surface integral
               0.1161399311023E+02 0.1161399311023E+02 0.3104879045267E-13
 Verification Successful


 LU Benchmark Completed.
 Class           =                        W
 Size            =               33x 33x 33
 Iterations      =                      300
 Time in seconds =                    95.18
 Total processes =                        4
 Compiled procs  =                        4
 Mop/s total     =                   189.75
 Mop/s/process   =                    47.44
 Operation type  =           floating point
 Verification    =               SUCCESSFUL
 Version         =                      2.3
 Compile date    =              12 Apr 2000

 Compile options:
    MPIF77       = f90 $(ABI)
    FLINK        = $(TAU_CXX)
    FMPI_LIB     = $(TAU_MPI_FLIBS) $(TAU_LIBS) $(LEXTRA1) $(T...
    FMPI_INC     = $(TAU_MPI_INCLUDE)
    FFLAGS       = -O3 
    FLINKFLAGS   = (none)
    RAND         = (none)


 Please send the results of this run to:

 NPB Development Team 
 Internet: npb@nas.nasa.gov
 
 If email is not available, send this to:

 MS T27A-1
 NASA Ames Research Center
 Moffett Field, CA  94035-1000

 Fax: 415-604-3957

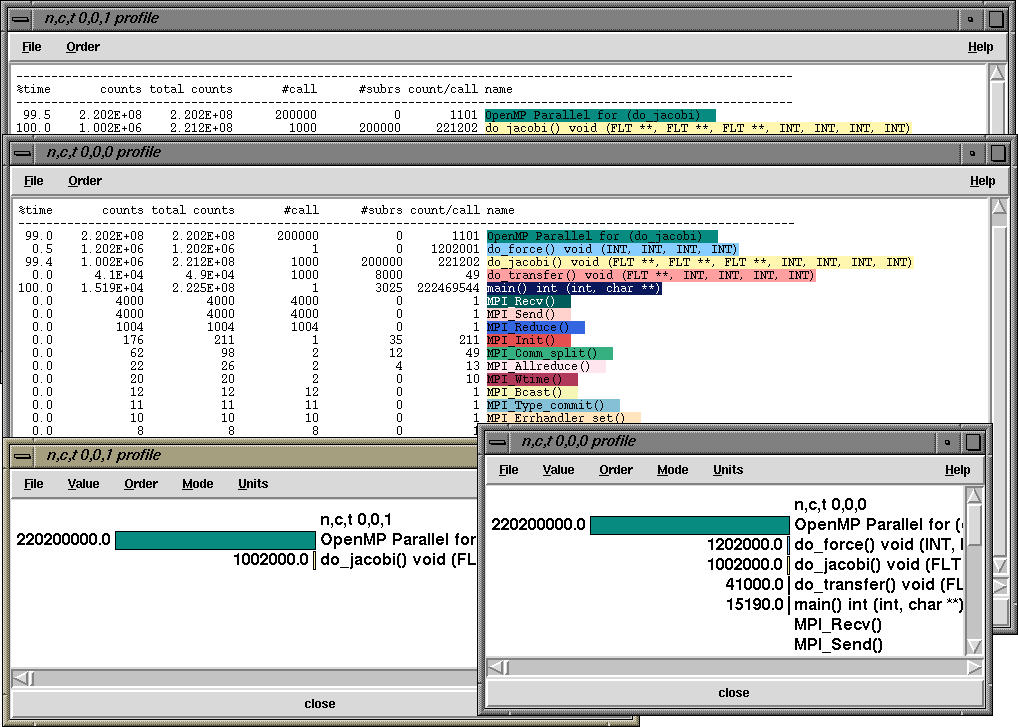
This generates the following profile on four processors of an SGI Power Onyx (eight R10000 194Mhz processors)

Explanation of the figure.

It shows that each of the processes have a similar profile. We can examine the inclusive and exclusive floating point instructions executed by each fortran and MPI routine on each processor, as explained below. n,c,t 1,0,0 means node 1, context 0, thread 0. For MPI, you may look at it as the "process with rank=1". The left top LU window shows the profile of four nodes (or four MPI tasks) and a "mean" profile. In this case, all nodes have similar contribution of routines which are represented in different colors. When you click on the "n,c,t 0,0,0" it brings up the profile of one particular node (rank=0 task). This is shown in the text window as well as the right top window, which shows the relative contribution of different routines. We're profiling for floating point operations. So, it shows the precise floating point operations executed in each routine. Exclusive count refer to the floating point operations (in this case) executed in the routine exclusive of all routines that it may call. For e.g., if foo calls f1 and f2.


        foo {

          f1(); -> takes 10 fp operations

          f2(); -> takes 20 fp operations
        }  ---> 100 operations from start to finish in foo

Then, foo has "inclusive count" of 100, and "exclusive count" of 70. If foo is called once and it calls 2 routines (f1 and f2), then we show calls for foo as 1 and Subrs for foo as 2. count/call shows the inclusive counts for foo/no. of calls.

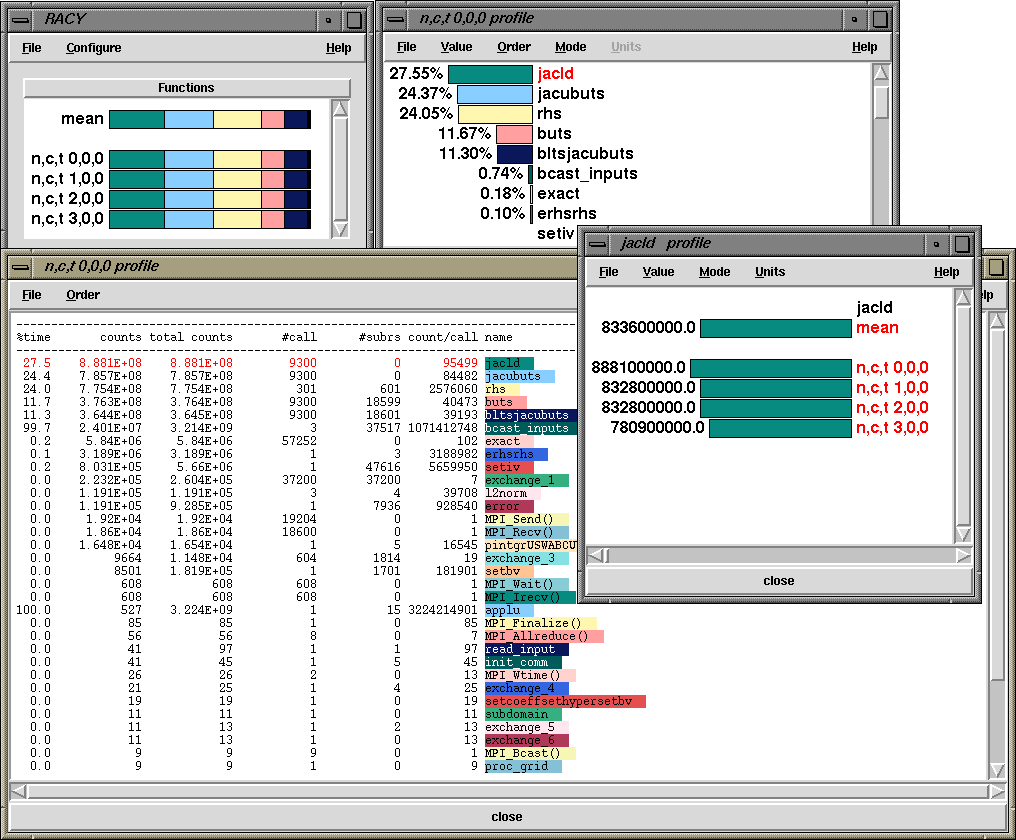
So, getting back to the display, the top right window shows that "jacld" accounts for 27.55% of total counts on that process. When I right click on "jacld" it brings up the jacld profile that shows me the profile of that routine on all nodes. So, we see that it had 8888100000 floating point counts on node 0, context 0, thread 0. We can choose from exclusive and inclusive options from the menu as well as percentage or real values. It also highlights (in red) the routine in all other windows. In the text window we can see that on node 0, context 0, thread 0, the routine "bcase_inputs" (shown in green) had 2.401E+7 exclusive counts and 3l214E+9 inclusive counts (99.7% of total). It was called 3 times and it in turn called 37517 other routines, and had an 1071412748 inclusive counts/call.

The user can get a similar explanation when the Help option is selected from the window.

More pictures

Examining the effect of data cache misses

To show the effect of data cache misses on an application, we code the classic matrix multiply algorithm in two ways. The "regular" way and by using a strip mining optimization with the loops interchanged to reuse "strips" of the resultant matrix and reduce data cache misses. The example program is run on a single processor of the SGI Power Onyx described above. It has 1GB of main memory (4-way interleaved), with 32KB of primary data cache and 32KB of instruction cache. It also has 2MB unified secondary data/instruction cache. The profile generated is shown below:

Notice how the regular matrix multiplication has 61% of the overall cache misses as opposed to just 13% for the strip mining optimization for multiplying two 512x512 matrices.