The Bitonic Sort Module


Next: The pC++ Program
Up: Program Analysis and Tuning
Previous: Introduction
To illustrate the programming tools in the  system we will focus on the
task of analyzing and tuning a single application based on a classical
parallel algorithm: Batcher's bitonic sort.
Sequentially sub-optimal, but a very parallelizable sorting algorithm,
bitonic sort is based on the bitonic merge, a natural application of
divide-and-conquer.
A bitonic sequence consists of two monotonic sequences that have been
concatenated together where a wrap-around of one sequence is allowed.
That is, it is a sequence
system we will focus on the
task of analyzing and tuning a single application based on a classical
parallel algorithm: Batcher's bitonic sort.
Sequentially sub-optimal, but a very parallelizable sorting algorithm,
bitonic sort is based on the bitonic merge, a natural application of
divide-and-conquer.
A bitonic sequence consists of two monotonic sequences that have been
concatenated together where a wrap-around of one sequence is allowed.
That is, it is a sequence

where 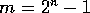 for some
for some  ,
and for index positions
,
and for index positions 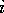 and
and 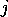 , with
, with  ,
, 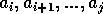 is monotonic and the remaining sequence starting at
is monotonic and the remaining sequence starting at 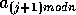 ,
where
,
where 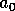 follows
follows 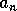 , is monotonic in the reverse direction.
See Knuth [1] for details.
, is monotonic in the reverse direction.
See Knuth [1] for details.
The bitonic merge can be stated in its most compact form as follows
input: an array of items a[0:2**n-1] containing a bitonic sequence.
merge(a, n, direction){
k = 2**(n-1)
foreach i in 0 to k-1 do
if(((direction == increasing) && (a[i] > a[i+k]) ||
((direction == decreasing) && (a[i] < a[i+k])))
swap(a[i], a[i+k]);
//now a[0:k-1] and a[k:2**n-1] are both bitonic and
//for all i in [0:k-1] and j in [k:2**n-1]
// a(i) <= a(j) if direction = increasing and
// a(j) <= a(i) if direction = decreasing
merge(a[0:k-1], n-1, direction); merge(a[k:2**n-1], n-1, direction);
}
Merging a bitonic sequence of length 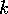 involves a sequence of data
exchanges between elements that are
involves a sequence of data
exchanges between elements that are 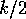 apart, followed by data exchanges
between elements that are
apart, followed by data exchanges
between elements that are 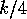 apart, etc.
The full sort is nothing more than a sequence of bitonic merges.
We start by observing that
apart, etc.
The full sort is nothing more than a sequence of bitonic merges.
We start by observing that 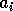 and
and 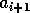 is a bitonic sequence of two
items for each even
is a bitonic sequence of two
items for each even 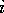 .
If we merge these length two bitonic sequences into
sorted sequences of length two and if we alternate the sort direction, we
then have bitonic sequences of length four.
Merging two of these bitonic sequences (of alternating direction) we have
sorted sequences of length 8.
This is illustrated in Figure 1 below where the vertical axis
represents time steps going down the page.
.
If we merge these length two bitonic sequences into
sorted sequences of length two and if we alternate the sort direction, we
then have bitonic sequences of length four.
Merging two of these bitonic sequences (of alternating direction) we have
sorted sequences of length 8.
This is illustrated in Figure 1 below where the vertical axis
represents time steps going down the page.
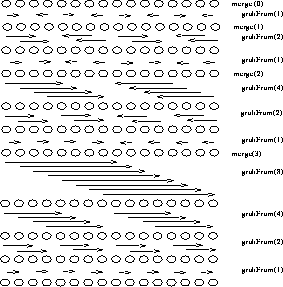
Figure 1: Data exchanges in the Bitonic Sort Algorithm
A data parallel version of this algorithm is given by
sort(a, n){
m = 2**n; // m = size of array
for(i = 1; i < n; i++){ // merge(i) step
k = 2**i;
forall(s in 0:m-1) d[s] = (s/k) mod 2; // d is the direction
for(j = k/2; j > 0; j = j/2){ // exchange(j) step
forall(s in 0:m-1) d2[s] = (s/j) mod 2;
forall(s in 0:m-1) where(d2[s]==1) tmp[s] = a[s-j];
forall(s in 0:m-1) where(d2[s]==0) tmp[s] = a[s+j];
forall(s in 0:m-1) where((d == d2) && (a > tmp)) a = tmp;
forall(s in 0:m-1) where((d != d2) && (a <= tmp)) a = tmp;
}
In an object parallel version of this algorithm we construct a set of
objects 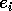 ,
, 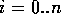 where each object contains a value from the
sequence
where each object contains a value from the
sequence 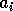 and a temporary variable
and a temporary variable 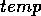 .
The exchange step in the merge is replaced by communication where object
.
The exchange step in the merge is replaced by communication where object
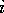 will grab
will grab 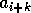 from
from 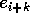 and store the value in
its temp variable.
In this operation,
and store the value in
its temp variable.
In this operation, 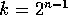 if
if 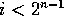 ;
; 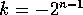 otherwise.
Once the values have been accessed and stored in the temporary variable, we
make a comparison and test.
Object
otherwise.
Once the values have been accessed and stored in the temporary variable, we
make a comparison and test.
Object 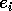 will replace
will replace 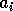 with the
with the 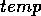 value if the appropriate
conditions are satisfied.
The code for this can be derived from the data parallel version of the
algorithm by rewriting it in terms of the action on a single array element
as described above.
As a C++ class this would appear as follows
value if the appropriate
conditions are satisfied.
The code for this can be derived from the data parallel version of the
algorithm by rewriting it in terms of the action on a single array element
as described above.
As a C++ class this would appear as follows
class ListItem{
public:
item a; // the data item
item temp; // a temporary value for the data swap step.
int direction; // a flag that store the direction of the current merge
int i; // the position of this object in the aggregate
ListItem *thisCollection; // a pointer to the collection
void merge(distance); // the bitonic merge
void sort(n); // the bitonic sort
void grabFrom(distance); // access the data from another ListItem
localMerge(dist); // the test and swap step
};
ListItem::sort(n){
for(d = 1; d < n; d++) merge(d);
}
ListItem::merge(int level){
direction = (i/(2**level) % 2;
for(int d = level-1; d >= 0; d--){
int distance = 2**d;
grabFrom(distance);
localMerge(distance);
barrier_sync(thisCollection);
}
}
item::grabFrom(dist){
if((i/dist) % 2) temp_data = thisAggregate[myPosition+dist].data;
else temp_data = thisAggregate[myPosition-dist].data;
}
ListItem::localMerge(int dist){
int d2;
d2 = (i/dist) % 2;
if((direction == d2) && (a > temp)) a = temp;
if((direction != d2) &&( a <= temp)) a = temp;
}
From the perspective of pC++ parallel programming, there is one very
critical point in the code above.
That is, there is a potential race condition in the merge step.
To see this, observe that if each object in the collection
is executing the merge function then, in the loop, one must make sure that
the data read operation in grabFrom executes after the other object
has completed the localMerge step of the previous iteration.
To enforce this rule we have inserted a barrier synchronization step
which causes all object to wait at this position before advancing to the next
iteration.
The insertion of this operation has serious impact on the asymptotic
complexity of this algorithm.
If there are 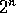 processors, the standard algorithm has time complexity
processors, the standard algorithm has time complexity
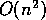 .
By adding the barrier synchronization, we have increased the complexity to
.
By adding the barrier synchronization, we have increased the complexity to
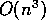 .
.
Another serious problem with the algorithm is that it is very inefficient
if the number of processors available is less than 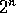 .
In the N-body application, we need to sort tens of millions of particles on
machines ranging from 8 to 1024 processors.
Consequently, we need a version of the algorithm that requires fewer
processors.
Fortunately, there is an easy way to increase the granularity of the
computation so that each object holds a vector of particles.
If we replace the
.
In the N-body application, we need to sort tens of millions of particles on
machines ranging from 8 to 1024 processors.
Consequently, we need a version of the algorithm that requires fewer
processors.
Fortunately, there is an easy way to increase the granularity of the
computation so that each object holds a vector of particles.
If we replace the ListItem class above with a class called
class Pvector{
item a[K]; // K is the size of the local vector
item temp[K];
...
};
and a standard quicksort function qsort(direction) to the
class that sorts the local vector of item in the given direction, then
the changes to the program are very small.
We only need to make sure that the initial vectors are sorted and that they
are resorted at the end of each merge step.
Pvector::merge(level){
direction = (i/(2**level)) % 2;
for(int d = level-1; d >= 0; d--){
int distance = 2**d;
grabFrom(distance);
localMerge(distance);
barrier_sync(thisCollection);
}
qsort(direction);
}
Pvector::sort(n){
qsort(i%2);
barrier_sync(thisCollection);
for(d = 1; d < n; d++) merge(d);
}
In addition to the changes above,
the function localMerge must be modified to operate on
a vector of data.
If we assume that the quicksort computation runs with an average execution
time of 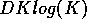 for some constant
for some constant 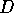 and
if we ignore the cost of the barrier synchronization,
and assume that there are
and
if we ignore the cost of the barrier synchronization,
and assume that there are 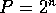 processors available and the size
of the list to sort is
processors available and the size
of the list to sort is 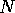 , then the time to sort is roughly
, then the time to sort is roughly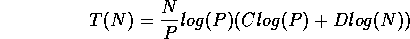
where 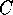 is a constant that depends upon communication speed.
Given a sequential complexity of
is a constant that depends upon communication speed.
Given a sequential complexity of 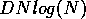 we see that
the parallel speed-up is of the form
we see that
the parallel speed-up is of the form
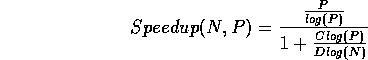
which, for large 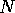 , is of the form
, is of the form 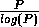 .
.
It is important to notice that at the end of each merge step, just
before the quicksort is called, the local vector is a bitonic sequence
due to its construction.
Hence, it is possible to apply a sequential bitonic merge that runs in time
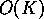 rather than the
rather than the 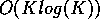 quicksort.
This changes the approximate execution time to be
quicksort.
This changes the approximate execution time to be
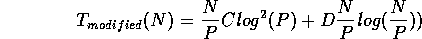
and the speed-up becomes
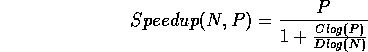
which, for large 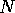 , is of the form
, is of the form 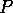 .
.
Our focus for the remainder
of this paper will be on using the  tools to explore several
questions about this algorithm posed by the analysis above.
In particular, we are interested in using the tools to consider the
following.
tools to explore several
questions about this algorithm posed by the analysis above.
In particular, we are interested in using the tools to consider the
following.
-
Does barrier synchronization adds a significant penalty to the complexity
that is not accounted for in the analysis above?
What percent of the time is actually spent in barrier synchronization for
problems of a size that is significant for the application?
-
Given that bitonic merge is communication intensive (in fact, the
bisection bandwidth of the communication graph scales linearly with
the problem size),
what percent of the time is spent in communication on different machines?
-
How significant is the improvement in the ``modified'' version of
the algorithm which replaces the quicksort in each merge step by a local
bitonic merge?


Next: The pC++ Program
Up: Program Analysis and Tuning
Previous: Introduction
Bernd W. Mohr
Thu Jan 5 14:01:02 PST 1995
 system we will focus on the
task of analyzing and tuning a single application based on a classical
parallel algorithm: Batcher's bitonic sort.
Sequentially sub-optimal, but a very parallelizable sorting algorithm,
bitonic sort is based on the bitonic merge, a natural application of
divide-and-conquer.
A bitonic sequence consists of two monotonic sequences that have been
concatenated together where a wrap-around of one sequence is allowed.
That is, it is a sequence
system we will focus on the
task of analyzing and tuning a single application based on a classical
parallel algorithm: Batcher's bitonic sort.
Sequentially sub-optimal, but a very parallelizable sorting algorithm,
bitonic sort is based on the bitonic merge, a natural application of
divide-and-conquer.
A bitonic sequence consists of two monotonic sequences that have been
concatenated together where a wrap-around of one sequence is allowed.
That is, it is a sequence
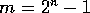 for some
for some  ,
and for index positions
,
and for index positions 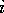 and
and 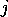 , with
, with  ,
, 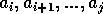 is monotonic and the remaining sequence starting at
is monotonic and the remaining sequence starting at 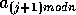 ,
where
,
where 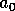 follows
follows 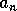 , is monotonic in the reverse direction.
See Knuth
, is monotonic in the reverse direction.
See Knuth 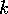 involves a sequence of data
exchanges between elements that are
involves a sequence of data
exchanges between elements that are 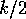 apart, followed by data exchanges
between elements that are
apart, followed by data exchanges
between elements that are 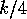 apart, etc.
The full sort is nothing more than a sequence of bitonic merges.
We start by observing that
apart, etc.
The full sort is nothing more than a sequence of bitonic merges.
We start by observing that 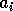 and
and 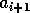 is a bitonic sequence of two
items for each even
is a bitonic sequence of two
items for each even 
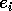 ,
, 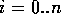 where each object contains a value from the
sequence
where each object contains a value from the
sequence 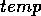 .
The exchange step in the merge is replaced by communication where object
.
The exchange step in the merge is replaced by communication where object
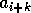 from
from 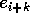 and store the value in
its temp variable.
In this operation,
and store the value in
its temp variable.
In this operation, 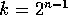 if
if 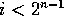 ;
; 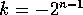 otherwise.
Once the values have been accessed and stored in the temporary variable, we
make a comparison and test.
Object
otherwise.
Once the values have been accessed and stored in the temporary variable, we
make a comparison and test.
Object 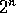 processors, the standard algorithm has time complexity
processors, the standard algorithm has time complexity
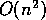 .
By adding the barrier synchronization, we have increased the complexity to
.
By adding the barrier synchronization, we have increased the complexity to
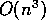 .
.
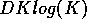 for some constant
for some constant 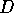 and
if we ignore the cost of the barrier synchronization,
and assume that there are
and
if we ignore the cost of the barrier synchronization,
and assume that there are 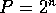 processors available and the size
of the list to sort is
processors available and the size
of the list to sort is 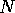 , then the time to sort is roughly
, then the time to sort is roughly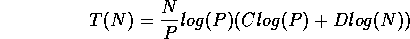
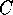 is a constant that depends upon communication speed.
Given a sequential complexity of
is a constant that depends upon communication speed.
Given a sequential complexity of 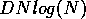 we see that
the parallel speed-up is of the form
we see that
the parallel speed-up is of the form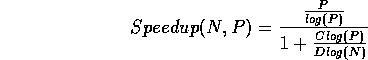
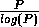 .
.
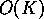 rather than the
rather than the 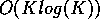 quicksort.
This changes the approximate execution time to be
quicksort.
This changes the approximate execution time to be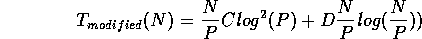
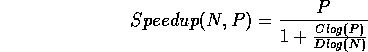
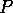 .
.