[Previous] [Top] [Next]

CHAPTER VIII
CASE STUDY: DATA DISTRIBUTION VISUALIZATIONS

In the preceding case study, the last example demonstrated a visualization that can be used for evaluating the distribution of a parallel data structure across processors. Such displays are important since many new parallel programming languages leave the task of data distribution primarily up to the programmer. This chapter develops a specialized visualization environment, based on the visualization methodology described earlier, that can assist in evaluating data distributions [5].

Introduction

New languages such as High Performance Fortran (HPF) [11] and the parallel C++, pC++ [1] offer cohesive data parallel programming abstractions, strive for efficiency, and have portability as an underlying motivation in their design. While these languages offer levels of abstraction far removed from the physical architecture, they still give the programmer explicit control over such issues as data distributions, data alignments, abstract processor arrangements, and specification of parallel loop constructs. The results are languages whose compilers capitalize on certain recent advances in compiler technology ([12], for example), but presently leave the critical task of distributing data across processors up to the programmer. There are those people who will undoubtedly applaud this step and consider user-specified data distributions a "feature." Equally likely, though, are those who will dread being forced to figure out the best way to partition manually their data structures. Giving this ability (or burden) to the programmer, places the performance of thousands of parallel applications in potential jeopardy. Clearly, the distribution of data across processors is a deciding factor in the performance of the program operating on that data. Thus, programmers using new languages such as HPF and pC++ could benefit from evaluating different data distributions.

The goal of this case study is to demonstrate how this new performance visualization paradigm can assist programmers requiring evaluations of data distributions. The work by Kondapaneni, Pancake, and Ward [20] demonstrates how data distributions and alignments in Fortran D (a language which contributed significantly to the design of HPF) may be specified using graphical representations of program data structures. They claim that the accuracy of data distributions specified by programmers using their visual programming tool were more accurate than those made by programmers who did not use the tool. Furthermore, the graphical environment encouraged experimentation with different mappings. These results strongly suggest that the evaluation of data distributions could benefit from graphical representations as well. To this end, the development of an experimental data distribution visualization (DDV) environment - a framework from which visualization techniques and evaluation criteria can arise - will be explored.

The rest of this case study will proceed as follows. First, a brief overview of the DDV project will be followed by a summary of the relevant aspects of High Performance Fortran. A particular application will be explored, and then some observations on the value of the visualizations which were generated will be discussed. Finally, some possible areas for future work and a summary will be given.

Goals for a DDV Environment

HPF and pC++ offer data parallel extensions to Fortran and C++, respectively, allowing programmers to specify data distributions for the data structures of each language. In HPF the programmer distributes arrays only. In pC++, traditional C++ objects are the targets of distribution specifications. As a starting point, this research focuses on developing visualizations for HPF. High Performance Fortran offers a simple platform from which to begin this work since only arrays need to be considered. With that in mind, two primary goals can be established.

First, metrics that will help the programmer determine the effectiveness of a given data distribution must be identified. Once this occurs, visualizations showing some or all of those metrics for a given distribution can be developed. Second, these visualizations should demonstrate some consistency with the programmer's mental model of the data structure, the distribution, or other aspects of the problem. This is a critical goal which deserves further explanation.

One of the primary features of HPF is that it offers an abstraction far removed from any particular architecture. Thus, the specific architectural knowledge required by the HPF programmer is far less than that required for other parallel environments. The consequence of this is that traditional performance visualizations based on physical processors and low-level message passing, for example, may not be as meaningful to the HPF programmer. Thus, visualizations for HPF must demonstrate levels of abstraction that are consistent with the language's - and hopefully the programmer's - underlying conceptual model.

High Performance Fortran

High Performance Fortran is a parallel Fortran language that offers support for high performance on a wide variety of parallel processing architectures, including massively parallel SIMD machines (e.g., Maspar's MP-1 or Thinking Machine's CM-2), distributed- and shared-memory MIMD architectures (e.g., the Intel Paragon and the Cray Y-MP C90), vector processors, and other architectures. Version 1.0 of the language specification [11] was released in May, 1993, by the HPF Forum, a coalition of industrial and academic groups representing most commercial vendors, several government labs, and many university research groups.

HPF is a set of extensions and modifications to Fortran 90 [15] to offer data parallelism in the form of explicit parallel loop constructs, code tuning for various parallel architectures through a set of extrinsic procedures, and high performance on MIMD and SIMD machines through data distribution and alignment capabilities which the user specifies with compiler directives.

The Programming Model

While there are many features of HPF which make it an interesting topic of discussion, this study is concerned only with its data distribution features. It is well known that modern parallel architectures achieve their best performance when data accesses exhibit high locality of reference. A programmer should, therefore, try to limit the frequency with which a processor must obtain data from other processors. Data distributions hold the key to achieving this goal. HPF allows the programmer to specify aspects of the distribution process. The primary directives and their functions are given in Figure 16.

HPF Directive Function
PROCESSORS Declare an n-dimensional mesh of virtual processors
ALIGN Specify relationships between multiple arrays
DISTRIBUTE Specify how arrays (or groups of arrays) are distributed across virtual processors
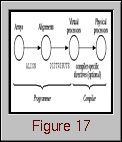
Figure 16. The primary compiler directives in HPF allow users to create virtual processors, align data structures, and distribute data across virtual processors.
The PROCESSORS directive allows the user to declare an abstract set of processors onto which distributed arrays are mapped. The abstract processor set takes the form of an n-dimensional mesh with no inherent interconnection network. Next, relationships between different data structures are specified with the ALIGN directive. An ALIGNment offers a common structure to which several arrays are oriented. Finally, using the DISTRIBUTE directive, ALIGNments (i.e., groups of related arrays) are mapped onto the abstract set of processors. Thus, the HPF programming model can be illustrated as in Figure 17 [11].

Figure 17. In HPF, programmers specify how data structures are distributed across a set of virtual processors, but the compiler is responsible for mapping virtual processors to the physical processing units of the computer.
From the programmer's perspective, this is a two-level mapping: first, data structures are aligned with one another, and then these groups of data structures are distributed onto a set of abstract processors. The compiler takes responsibility for mapping the abstract processor set onto the physical processors. (The HPF Forum suggests that commercial HPF compilers may wish to offer compiler-specific directives so that the user has some say in how abstract processors are mapped to physical processors.) From this, the underlying programming model becomes evident. Programs are written as if running on an arbitrarily sized, n-dimensional mesh of processors. This is consistent with the ideal data-parallel programming paradigm where the amount and type of data determines the processing resources needed.

The HPF model is dependent on two assumptions that are reasonable for current architectures. First, an operation involving multiple data elements will be faster if the elements are all on the same processor. Second, many such operations can be done simultaneously if they can be performed on different processors.

Computations in HPF

The final aspect of HPF which must be addressed is the manner in which computations are carried out. Bozkus et al. [2] propose four possible models of computation based on the locations of left-hand and right-hand data operands. Given the generalized form of an assignment statement, A: lhs = rhs, Figure 18 illustrates four possible cases.

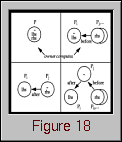
Figure 18. On a distributed-memory parallel computer, an assignment statement can be carried out using four techniques.
Pi denotes processor i. The processor containing "lhs" owns the data element on the left-hand side of the assignment; the processor(s) with "rhs" owns data elements which are required by the computation; the processor containing the "=" is the processor which performs the computation. Annotated arrows indicate the interprocessor communication required with respect to when the computation is performed (i.e., before or after).

Given a data distribution, the processor responsible for performing a computation is not specified by HPF; that is, it is up to the compiler to determine which processor will perform a given computation. As noted in Figure 18, one of the more popular parallel computation models is known as owner computes. Under this scheme, the processor which "owns" the left-hand side data element (i.e., the data element to which the assignment is being made) is the one that performs the computation. Thus, before the computation can occur, all data elements which occur on the right-hand side of the assignment and reside on remote processors must be copied into the owner processor. A degenerate case of owner computes occurs when all data elements are locally owned. Thus, the top half of Figure 18 illustrates cases of the owner computes rule.

Since the manner in which assignments and computations are carried out is compiler-dependent, this work will generally assume that the owner computes rule is used. This assumption is evident only in the sample application described later.

Establishing the DDV Problem Domain

As shown in Figure 19, establishing a problem domain for data distribution visualization consists of deciding which HPF features will be addressed by the visualizations, how data distributions are to be evaluated, and what properties the visualizations should have. The following sections will identify and justify the decisions which were made.

Figure 19. The DDV problem consists of three main issues.

High Performance Fortran

For this case study, it is important that the problem be accessible. For this reason, visualizations are limited to two-dimensional data arrays and two-dimensional sets of processors. This results in simple, obvious mappings from data structures and processor sets to graphical objects. (Similarly, an upper-bound of three dimensions was set in [20].)

In addition, data structure alignments are not considered. The current visualization system considers only individual arrays. Thus, relationships to other arrays, specified with the ALIGN directive, are currently irrelevant, though such relationships could undoubtedly play a role in future performance visualizations.

In HPF, programmers can dynamically redistribute arrays in the middle of their program. To maintain simplicity, DDV considers static distributions only.

Finally, as mentioned earlier, the owner computes rule will be assumed as the computational model for the sample application.

Evaluation of Data Distributions

The evaluation of data distributions is essentially a load balancing problem. The programmer wants to make sure that data structures are distributed in such a way that no single processor is excessively burdened with data requests. In accordance with the assumptions underlying HPF, the programmer also wants to maximize local data accesses and minimize the number of remote data operations that a given processor must perform. To evaluate a data distribution for a given application, the programmer needs to formulate answers to two questions:

  • What memory reference patterns are exhibited by the application?
  • Given the data distribution, how do these reference patterns manifest themselves on the set of processors?

Thus, it stands to reason that the type of accesses being made to data structures (i.e., reads or writes) and the type of communication associated with that operation (i.e., local or remote) will play an important role in determining whether a given distribution is good or bad. If visualizations can be devised that show reference patterns for both the data structure and the processors across which the data is distributed, then the HPF programmer can answer the questions above. To this end, DDV focuses on collecting information about data reference patterns, and then determines which processor has a given data element under the specified data distribution. Note that "processor," unless otherwise stated, refers to "virtual" processor during the rest of this chapter. Since HPF will potentially run on many different architectures, visualizations based on virtual processors are not architecture-specific.

Visualization Characteristics

One of the primary goals set out earlier in this thesis was that visualizations should incorporate the programmer's mental model. This applies to both data structures and processors. The limitations applied to HPF described above make this task much easier. By placing an upper-bound of two dimensions on arrays and processors, visualizations should be able to include easily the traditional representation of arrays. The creators of the visual programming tool for Fortran D [20] point out the importance that should be placed on maintaining consistency between graphical portrayals of arrays and the programmer's mental model of arrays. They indicate that a grid of cells arranged in rows and columns is the most obvious and intuitive representation of such structures.

In order to answer fully the questions posed above, visualizations should incorporate the passage of time. In general, this means that there should be some component of animation in the visualizations. (Although, time can be incorporated into visualizations in other ways, as was done in Chapter VII.)

Finally, the ability to show multiple dimensions of the problem in a single visualization may be useful in some circumstances. At the very least, this should be an option for the programmer.

Given the establishment of the DDV problem domain, the problem at hand is well-defined and approachable. We now turn to a discussion of the experimental environment which was developed within the parallel program and performance visualization methodology that is the topic of this thesis.

An Experimental DDV Environment

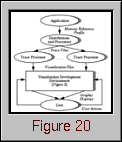
In the following sections, a detailed examination of the DDV environment will be presented. Figure 20 offers an overview of the steps from application to visualization.

Figure 20. The DDV environment incorporates the implementation environment of Figure 2 by adding capabilities for collecting and processing trace and performance data.

Creating Memory Reference Profiles

As with the visual programming tool for Fortran D [20], DDV encourages the programmer to experiment with different distributions for a given application. As shown in Figure 20, the first step in this process is to create a memory reference profile for an application. The current environment does not actually handle parallel programs since no HPF compiler was readily available at the time of this work; rather, a sequential application is used to mimic a parallel one, and the owner computes rule is imitated by calls to a TRACE function (see below). At desired points in the code, function calls are inserted to generate profiling information about the particular memory operation(s) being performed and the data elements being referenced. To mimic owner computes, the profiling information is made relative to some other data element - in particular, the element appearing on the right hand side of the assignment. This process can be accomplished automatically with current program transformation technology.

While the profile may not actually represent the parallel execution, it identifies the reference patterns that an application exhibits. Better yet, the reference profile is independent of any particular data distribution. Thus, a single profile can lead to the creation of any number of trace files which are distribution-specific. If a real parallel application was to be used, then the TRACE function could be easily modified to generate distribution-specific information, and the memory reference profile would be unnecessary.

The TRACE function accepts a time stamp, the location of the "owner" element, a range of referenced data elements, and the operation (read or write) performed. (Note that whether the operation required local or remote communication is unknown until a distribution is specified in later steps.)

Building Trace Files

Once a memory reference profile has been established, any number of trace files can be generated. Each trace file is specific to a single data distribution and processor arrangement. Thus, the process of building a trace file requires a filter program that understands HPF's data distribution functions. The HPF language specification [11] offers formulaic definitions of the distribution options discussed earlier in this paper. These formulas provide the mapping from data elements to processors in a single dimension.

First, define c(j,k), the ceiling division function, by c(j,k) = FLOOR((j+k-1)/k). Let d represent the size of the data array in a certain dimension, r, and let p be the size of the corresponding dimension in the processor array. (Assume all dimensions have a lower bound of 1.) Then, the specification BLOCK(m) means that data element j of dimension r will be mapped to the abstract processor at location c(j,m), provided that mp >= d. Similarly, CYCLIC(m) means that the data element in location j of dimension r will be owned by processor 1+((c(j,m)-1) MOD p). These relationships are used to transform a memory reference profile into a trace file once a data distribution has been specified. The trace file allows for multiple operations in a given time step. In this fashion, the annotation of a sequential application can be used to mimic the operation of the parallel application.

Creating Visualization Files

The next step to data distribution visualizations is to transform the trace file into a visualization file. From the information in the trace files discussed above, this step keeps track of running totals and averages of local reads, remote reads, local writes, and remote writes for each element in the data array and the processor set. This information is present for each time step in the trace file. Thus, the totals and averages are computed over the time that has expired up to that point in the trace. In this way, an animation of the application's memory references may be constructed in the visualization environment.

Building a Visualization Framework

The final step in the visualization process is to use the data visualization software to create an environment for exploring the data distribution visualization. As mentioned in Chapter VI, Data Explorer allows the user to create control panels. The one in Figure 5 came from the DDV environment.

The visualizations display two views (cumulative and average) of a given trace quantity. One statistic is mapped to a colored background on the grid, and the other is mapped to "glyphs" which float in front of the grid. (The graphic displays will be discussed in more detail later.) The user can control several aspects of the display:

  • The trace type to view (data or processor)
  • The dataset to view (the user can easily add additional traces to the control panel)
  • The quantity to be displayed display (e.g., local reads, all remote accesses, all reads and writes, etc.)
  • The statistics to be displayed (cumulative and/or average)

The user can also control the animation with the "Sequence Control" box. The controls are simple and intuitive, similar to those used in audio cassette and compact disc players.

In the actual visualizations, quantities are represented by the size and color of the glyphs, and by the color of the background grid coloring. (Note that glyphs contain redundant information. That is, the size and color of the glyph represent the same quantity.)

Application: Gaussian Elimination

To demonstrate the effectiveness of these visualizations, a sample application will be presented here. As was mentioned earlier, the current DDV environment is set up to operate with sequential programs. By carefully annotating this code, a pseudo-parallel trace file can be generated.

The Data Distribution

In the following, visualizations built from a Gaussian elimination algorithm will be presented. The algorithm operates on a 10x10 data array which is distributed on a 2x8 grid of processors in a cyclic fashion (for both rows and columns). The quantity being displayed in the images consists of all memory accesses (that is, local and remote, reads and writes).

Let us consider the distribution of data which results from the distribution and processor arrangement given above. Figure 21 specifies the processor which owns each element of the 10x10 array by assigning each processor a unique number. It is important to note that processors 0, 1, 8, and 9 own many more elements than the other processors because columns are distributed in a cyclic manner.

Figure 21. The cyclic distribution of a 10x10 array onto a 2x8 grid of processors leaves some processors more heavily loaded with data elements.

Source Code Instrumentation

A fragment of code from the Gaussian elimination algorithm used to generate the visualization presented in the following sections appears in Figure 22.

c = 1.0/B[j][j];
  for (col=0; col<MAX; col++) {
    /* scalar mult. the elements of row */
    B[j][col] = c*B[j][col];

    /* each owner read a copy of B[j,j] */
    TRACE(Time, j,col, j,j, j,j, 0);
    /* read own copy of B[j,col] */
    TRACE(Time, j,col, j,j, col,col, 0);
    /* write B[j,col] */
    TRACE(Time, j,col, j,j, col,col, 1);

    /* do the same to the augmentation */
    M[j][col] = c*M[j][col];
  }
Time++;
Figure 22. An instrumented code fragment shows how the sequential algorithm is used to imitate a possible parallel implementation.
The piece of code illustrates the transformation that takes place during the instrumentation process. The loop is one part of the Gaussian elimination algorithm. In this example, each row is being scaled by the reciprocal of the element on the main diagonal. While the sequential algorithm makes an assignment to the variable c, the calls to TRACE mimic what might actually happen in a parallel version of the algorithm by having each of the "owners" - referenced by the data element at (j,col) - request copies of that value. Note also that the Time variable is not incremented until after the loop, suggesting that the operations in the for-loop could be done simultaneously in a parallel implementation.

Display Generation

The instrumentation is compiled along with the source code, and a file containing a stream of memory references augmented with some additional information results after the application is run. This memory reference profile is independent of any data distribution, and it represents the pattern of memory accesses that this implementation of Gaussian elimination displays under a loose interpretation of the owner computes rule. The profile is used to create several different traces - one for each distribution and processor set that the user wants to evaluate. The trace files are then transformed into visualization files and imported into Data Explorer where the user can control many aspects of the resulting animation, as explained in the earlier parts of this thesis.

Visualizations

At this point, we are finally prepared to present a sequence of actual visualizations which resulted from the Gaussian elimination program.

Figure 23 illustrates the data array early in the execution of the Gaussian elimination algorithm (time 20). The background represents the average number of memory references, while the glyphs (size and color) keep track of the cumulative number of references. With element (0,0) in the upper left corner, the access patterns of this phase of the algorithm are already evident. As the algorithm proceeds, the glyphs in each column below the main diagonal grow larger (and change color) as the column elements below the diagonal are zeroed-out, and the row elements are adjusted accordingly.


Animation (277K)
Figure 23. (Time 20) Data access patterns are already evident early in the algorithm.
Figure 24 displays the state of the processors at the same time as Figure 23. It can be seen that the size of the glyphs on the left side of the grid are slightly larger than the others, however, it is too early to tell if this is due to a poor distribution or the particular phase of the algorithm.


Animation (49K)
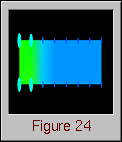
Figure 24. (Time 20) The processors do not yet appear too unbalanced.
Figure 25 shows the data array at time 60 of the algorithm. The first phase of the Gaussian elimination has been completed, and the second phase is just beginning. Thus, all of the elements on the main diagonal are now 1, and all elements below the diagonal are 0. The algorithm is proceeding to zero-out all matrix elements above the main diagonal by working its way back through the columns in reverse order, toward the origin of the array. Figure 26 shows a different quantity being displayed on the data array. Rather than showing all memory references, Figure 26 shows only remote writes, the pattern of which is considerably different than the overall memory reference pattern illustrated by Figure 25.


Animation (277K)
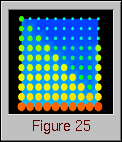
Figure 25. (Time 60) The visualization reflects the beginning of the second phase of the Gaussian Elimination algorithm.
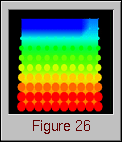
Figure 26. (Time 60) The distribution of remote writes is considerably different than the overall distribution of all memory accesses.
Figure 27 again shows the status of the processor grid. The imbalance generated by the cyclic distribution is becoming more and more evident at this point in the animation. The other processors appear to be fairly well-balanced, though.


Animation (49K)
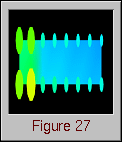
Figure 27. (Time 60) A growing imbalance in processor load becomes evident.
By time 89, as seen in Figure 28, the algorithm is nearing completion with only two columns remaining to be processed. It is evident from this display that overall, the Gaussian elimination algorithm accesses the array in a fairly uniform manner. That is, there are no elements that receive excessive attention in the long run. However, the earlier frames of the animation clearly show that the algorithm progressed in certain phases.


Animation (277K)
Figure 28. (Time 89) The algorithm nears completion, and the display seems to suggest a fairly uniform access pattern over the life of the algorithm.
Finally, Figure 29 illustrates the sorry state of the processor grid by the end of the algorithm. The load imbalance introduced by the cyclic distribution has clearly overtaxed the processors in the two left columns of the grid.


Animation (49K)
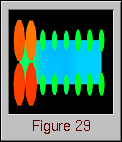
Figure 29. (Time 89) Processors in the left two columns of the grid have experienced significantly more memory accesses than the others.
Some conclusions regarding the effectiveness of a cyclic distribution in this case have already been made. Using what has been learned and the DDV tools discussed earlier, the programmer could now go back and create a new trace file using a different distribution or a different processor arrangement. In this way, experimenting with different distributions is simplified and the programmer undoubtedly gains insight not only to the algorithm, but to which distributions are most effective for it.

Observations

In this section, some informal observations on the effectiveness and utility of the DDV environment, as implemented within the more general parallel program and performance visualization methods discussed earlier, will be made. This will take place in three categories: usefulness, understandability, and scalability.

Usefulness

As was shown in the previous section, the visualizations generated from the DDV environment provided a good overview of memory reference patterns exhibited by the application. Depending on the quantity that the programmer is viewing, a sense of the interprocessor communication required is easily achieved. By offering the programmer visualizations of both the data structure and the processor set holding the data, one can effectively assess many characteristics of a given data distribution.

While reference patterns can be extracted directly from the animated displays, the size of messages being passed between processors remains obscured. Similarly, contention for data elements can not be seen. While this study has not focused on these metrics, they are still of potential interest to programmers.

Understandability

Since the problem domain limited the data structures and processor arrangements to two dimensions, these displays were able to take advantage of the obvious way to visualize such structures (i.e., by using a grid). For this reason, the displays are fairly simple to understand. The images shown here clearly lack labelling that would be present in a more complete environment, though. For example, the actual DDV displays contain captions and color bars for each quantity being measured.

It was mentioned earlier that the glyphs contain redundant information by having the size and color controlled by the same quantity. This could have both positive and negative effects. To novice users, it may reinforce the magnitude of the particular quantity. This technique is called "double cueing." More advanced users might find double cueing redundant and would prefer having color and size each represent a unique metric. The visualization environment is flexible enough to handle both cases.

Scalability

Finally, a very important topic in performance visualization is the scalability of the displays, especially in the context of data-parallel programming. Certain aspects of these visualizations are scalable while others are not. The glyphs, for example, do not offer a high degree of scalability. While very effective for small grids, the information is lost when grid size goes much above twenty in one dimension. In particular, the variance in the size of the glyph becomes so minute that little or no information is conveyed and visual complexity becomes excessive. Thus, glyphs may be more appropriate for processor sets since they tend to be smaller than data arrays.

The background grid coloring represents a more scalable visualization technique, however. By letting the color of the grid at each data element correspond to the quantity being measured, a global picture of memory references can be achieved for both small and large grids. In fact, the display actually seems to improve as the grid grows larger, up to a certain point. By letting the appropriate quantities color the grid background, the "hot" and "cool" spots of the data structure emerge. Also, data visualization software offers zooming capabilities which allow the user to focus on particular regions of the data or processor structure. The issue of scalable visualizations will be explored in detail in the final case study in Chapter IX.

Summary

The work presented here can be extended in several ways, especially since a very limited problem domain was pursued for this case study. The visualizations presented in this case study have as a primary goal the maintenance of consistency with the programmer's conceptual model. While these visualizations do not make full use of the data visualization software's graphical capabilities, the DDV environment, as a whole, does take advantage of the customization and interactive features of the software. Other visualization techniques that preserve consistency and make use of more sophisticated visualization techniques are also possible. Figure 15 presented in Chapter VII, for example, uses a rubber sheet in which grid points are displaced a distance proportional to some performance metric.

Still other visualizations may choose to deviate from the consistency goal to reveal relationships that are not evident in a simple two-dimensional grid. It is still important that the programmer have access to displays like the ones presented here, but there could be much to gain from advanced displays which are not necessarily formulated from a programmer's conceptual view. Such extensions to data distribution displays are pursued in Chapter IX which deals with scalable performance visualizations for data-parallel programs in general.

The important role played by data distributions in determining the efficiency of parallel applications demands that tools which assist in evaluating data distributions be developed. This case study has developed an experimental environment that explores the use of visualization for the evaluation of data distributions. It has been demonstrated that visualization techniques can be developed that will benefit the programmer responsible for writing efficient HPF programs.

Last modified: Wed Jan 20 15:14:29 PST 1999
Steven Hackstadt / hacks@cs.uoregon.edu